This was a lot of fun. Ever hear of a video game called Tron? Well, the University of Waterloo held an Artificial Intelligence challenge based on it. The level of participation was way higher than I ever expected it would be. I’m sure that the fact Google was sponsoring the challenge had something to do with the interest. In the end, I placed 49th out of approximately 800 participants. My language of choice was C#. And, my entry was 4th best out of the C# entries. The final results clearly illustrate one of the difficulties with this challenge. There are only 708 rankings shown. Therefore, it can be concluded that almost 100 participants were disqualified for exceeding the 1 second time limit between moves.
Using Tron was a great choice for the challenge. It’s a simple game with simple rules:
- It’s a 2 player game
- The players are situated on a map enclosed by walls. Maps are no larger than 50x50 squares
- Each player can move in one of 4 directions: north, east, south, or west. But, for any given position, a player only has a maximum of 3 of the 4 choices (unless they are suicidal)
- Running into a wall results in a loss for that player. If players run directly into eachother, it’s a draw
- When each player moves, a trail is left behind. Thus, a player’s previous position turns into a wall. (the reason why at any given position a player only has a max of 3 different moves).
- And, two additional constraints for our challenge: limit of one thread of execution and no longer than 1 second between moves
Sounds simple enough, right? But, what if you were asked “How would you create a smart Tron computer player?” Still simple? Now, it’s not as difficult as say creating a computer chess player. And, that’s the other reason why this problem is so intriguing. It’s simple enough to appeal to beginners and complicated enough for seasoned programmers.
I am by no means well versed in Artificial Intelligence, or AI, for short. I’ve taken a course in university that introduced me to graph problems such as the problem of “The farmer, goat, wolf, and cabbage” Why is that applicable? Because the Tron map can be thought of as a graph. Each square on the map is a node in the graph. Each direction a player can move in represents edges between nodes. In the above mentioned course, I was introduced to algorithms such as depth-first and breadth-first search and problems likc shortest path and longest path between graph nodes. All of which are very applicable to the game of Tron. So, with my AI text in hand and Wikipedia a click away, I decided to take a shot at creating an intelligent Tron bot.
One can think of Tron as a game requiring one of two basic strategies:
- Chase your opponent and attempt to box them into a small space
- Conserve as much space as possible, at all times
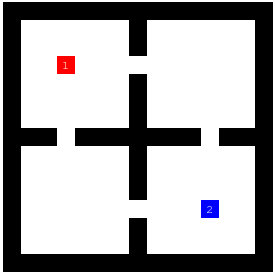
Conserving space right from the start can leave you vulnerable to being boxed into a corner. Therefore, it seems like a smart idea to attempt to chase your opponent into a corner. However, after viewing some games on a variety of different maps, it becomes clear that this is not always the best strategy. Take the below map, for example:
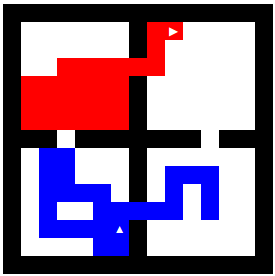
As you can see, if player 2 chooses to chase player 1 while player 1 conserves its immediate space, player 2 will block themselves into a smaller area than player 1. Then, player 1 can block player 2 off and continue conserving its space until player 2 runs into a wall. Here is a good example game of where I employ player 1’s strategy successfully. And, a screenshot of the endgame is shown below:
So, it becomes clear that the problem is space. Part of a highly successful strategy would be to maximize the amount of space you can reach over that of what your opponent can reach. I chose to employ that strategy by using alpha beta pruning with iterative deepening. My evaluation function for the alpha beta algorithm determines which player has the space advantage. This allows me to always try to move into the area that will give me the space advantage over my opponent. By using iterative deepening, I can watch the clock at each iteration. So, if I get close to using up 1 second of time, I can quickly return the best move calculated so far.
I should point out that I was not the only one using this idea of maximizing space. A lot of the bots used alpha beta with some variation on the “my space vs. opponent space” evaluation function. So, this idea is not all that original.
Below is my _Territory _class that I instantiate and use from my evaluation function to calculate each players’ space:
sealed class Territory
{
private GameState gs;
private Point me;
private Point you;
private int[,] map;
private int mySize = 0;
private int opponentSize = 0;
private const int BOUNDARY = 9999;
public Territory(GameState gs)
{
this.gs = gs;
this.me = new Point(gs.MyX(), gs.MyY());
this.you = new Point(gs.OpponentX(), gs.OpponentY());
}
// modified flood fill to scan outwards from each players' locations
// and mark their territories
private void scan()
{
map = new int[gs.Width(),gs.Height()];
Queue<Point> q = new Queue<Point>();
q.Enqueue(me);
q.Enqueue(you);
map[me.X,me.Y] = 1;
map[you.X,you.Y] = -1;
int player = 1;
int level = 1;
while(q.Count > 0) {
Point node = q.Dequeue();
if (node.X < 0 || node.Y < 0 || node.X >= gs.Width() || node.Y >= gs.Height())
continue;
// exclude first nodes from this check
if (Math.Abs(map[node.X, node.Y]) != 1 && gs.IsWall(node.X, node.Y))
continue;
level = map[node.X, node.Y];
// already marked as BOUNDARY so skip
if (level == BOUNDARY)
continue;
// check player: + us - opponent
if (level > 0) {
player = 1;
} else if (level < 0) {
player = -1;
}
// bump level
level = Math.Abs(level) + 1;
//Console.Error.WriteLine("x " + node.X + " y " + node.Y + " value " + map[node.X, node.Y]);
// process the neighbours
Point north = new Point(node.X, node.Y-1);
if (ProcessNeighbour(north, level, player))
q.Enqueue(north);
Point east = new Point(node.X+1, node.Y);
if (ProcessNeighbour(east, level, player))
q.Enqueue(east);
Point south = new Point(node.X, node.Y+1);
if (ProcessNeighbour(south, level, player))
q.Enqueue(south);
Point west = new Point(node.X-1, node.Y);
if (ProcessNeighbour(west, level, player))
q.Enqueue(west);
}
}
private bool ProcessNeighbour(Point node, int level, int player)
{
if (node.X < 0 || node.Y < 0 || node.X >= gs.Width() || node.Y >= gs.Height())
return false;
if (gs.IsWall(node.X, node.Y))
return false;
int val = map[node.X, node.Y];
if (Math.Abs(val) == 1)
return false;
// already processed by other player and levels are equal so define boundary
// of territory and do not process its neighbours
if (val != 0 && val != BOUNDARY && val * player < 0 && Math.Abs(val) == level) {
map[node.X, node.Y] = BOUNDARY;
// adjust size when area is marked as boundary
if (player > 0) {
opponentSize--;
} else {
mySize--;
}
return false;
// unprocessed and our terrirtory. mark and visit neighbours
} else if (val == 0 && player > 0) {
map[node.X, node.Y] = level;
mySize++;
return true;
// unprocessed and opponent territory. mark and visit neighbours
} else if (val == 0 && player < 0) {
map[node.X, node.Y] = -level;
opponentSize++;
return true;
}
// otherwise, do not visit neighbours
return false;
}
public int GetMySize()
{
return mySize;
}
public int GetOpponentSize()
{
return opponentSize;
}
public void DetermineTerritories()
{
scan();
}
}
It is simply a modified flood fill algorithm (more details on flood fill below) that processes both players at the same time. The Point class is basically just a wrapper around an x and y coordinate. The GameState class maintains the current state of the map, player positions, next moves, etc.
This is only part of my overall strategy, however. Once the opponent has been boxed in, the opponent no longer needs to be considered. Therefore, it makes sense to employ another strategy to conserve the remaining space. I chose to base this strategy on an algorithm called Flood Fill. Below is the method I used:
private static int FloodFill(GameState gs, int x, int y)
{
Queue<Point> q = new Queue<Point>();
int total = 0;
// shallow copy array
bool[,] map = (bool[,])gs.map.Clone();
q.Enqueue(new Point(x,y));
map[x,y] = false;
//Console.Error.WriteLine(x + " " + y);
while(q.Count > 0) {
Point n = q.Dequeue();
if (n.X < 0 || n.Y < 0 || n.X >= gs.Width() || n.Y >= gs.Height())
continue;
// process neighbours, mark as visited and increment count
if (!map[n.X, n.Y]) {
q.Enqueue(new Point(n.X+1, n.Y));
q.Enqueue(new Point(n.X-1, n.Y));
q.Enqueue(new Point(n.X, n.Y-1));
q.Enqueue(new Point(n.X, n.Y+1));
map[n.X,n.Y] = true;
total++;
}
}
return total;
}
As you can see, the flood fill is essentially a breadth-first search that counts the total number of reachable squares on the map. I run a depth-first search in each of the possible directions from my player’s position. Each search returns a cumulative flood fill count for the associated direction. The direction with the highest count is the best move. In the event of ties, the direction closest to a wall is chosen. This technique works rather well. However, it has its shortcomings.
Take the below map, for example. The red player has a decision to make: does it fill the area on the right or the left first?
My bot, unfortunately, decides to fill the area on the left first. This results in a lot of wasted space. And, of course, a loss.
I haven’t really analyzed where my algorithm goes wrong. But, I am sure that it can be improved. There are other techniques I would have liked to have experimented with:
- Connected components - a Tron map can be thought of as a graph that can be broken up into components. Knowledge of the number and size of these components can be helpful for determining which areas are dead ends. And, if only one of those dead ends can be visited by a player (which I think is always the case), then the largest of the dead ends can be used to calculate an optimal path
- Articulation vertices - the above mentioned components could be identified by articulation vertices. If the removal of any node in the graph results in an increase in the number of connected components, then the nodes neighbouring the cut vertex can be counted and defined as a component
- Heuristic history - basically a cache of previous game state evaluations. Caching would save computation time on successive iterations of the alpha beta algorithm
- Move ordering - the alpha beta algorithm is most efficient when searching best moves first. So, saving and sorting the game state tree would be beneficial
To me, it seems as though a sound addition to my strategy would be to avoid dead ends identified by components and articulation vertices, avoid creating new articulation vertices, and hug walls as much as possible. The heuristic history and move ordering are more for the alpha beta strategy to allow for a deeper search. And, therefore, should improve decision making when seeking space.
Of course, I have none of these ideas very well formed. However, a few of the contest participants implemented some mix or variation of these ideas with great success. Some even went in a totally different direction by attempting to use Monte Carlo, a commonly used strategy in AI engines for the game Go. It has definitely been very interesting seeing the different strategies of all the great minds involved exposed. I have learned a lot, it was fun, and I’m very glad I participated.
There is some talk of U of W opening the server up for new submissions on a “for fun” basis. So, I may have a chance to see if I can incorporate these ideas and make my bot even smarter. I’m not really sure how I feel about that, though. Having another chance at improving my bot is a very dangerous thought, as this can be very addicting!